Intro
I- Définitions
1/ Enthalpie libre standard molaire
2/ Gaz parfait
3/ Mélanges idéaux ou réels
II- Expressions du potentiel chimique
1/ Gaz parfait
2/ Corps pur condensé
3/ Mélanges idéaux et réels
III- Propriétés et applications
1/ Equilibre entre deux phases
2/ Les lois de l'ébullioscopie, cryoscopie et osmose
Conclusion
En version plus
développée...
Intro :
Les outils thermodynamiques sont U et H pour le premier principe, et G et F pour le second principe. Le potentiel chimique découle de l'étude des variations de ces fonctions dans un système en réaction.
I- Définitions
1/ Enthalpie libre standard molaire
Voir chapitre les outils thermodynamiques de l'évolution III- Le potentiel chimique 1- et 2-
Rappeler les expressions de dU, dH, dG , dF en fonction des deux variables parmi (S , V) (S,P) (T,P) (T,V) et en fonction des dni . Rappeler au passage que ( ∂G/∂P)T = V
Montrer alors que les 4 termes ( ∂X/∂ni)..,..,nj sont égaux , en particulier à l'un, pratique : (∂G/∂ni)T,P,nj = μi(T,P) = gi
2/ Gaz parfait
Rappeler la définition d'un gaz parfait : aucune intéraction entre les molécules de gaz : PV = nRT
3/ Mélanges idéaux ou réels
Si étude liq / vapeur, il existe 2 types de graphes donnant PA ou PB en fonction de la composition de la solution, à une température donnée T .
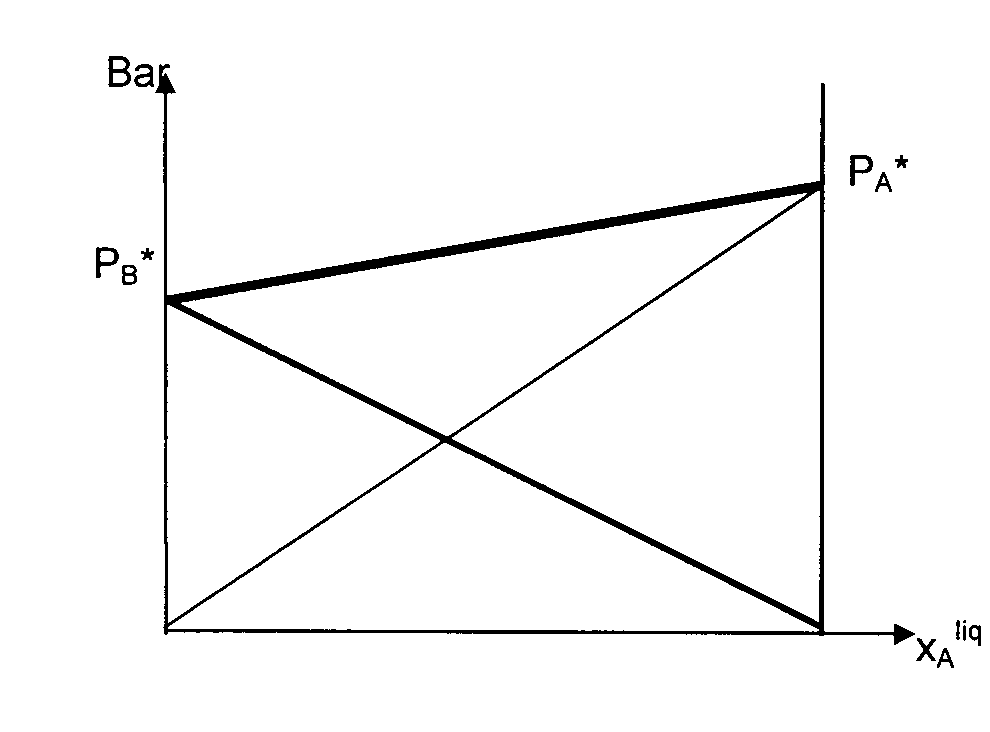
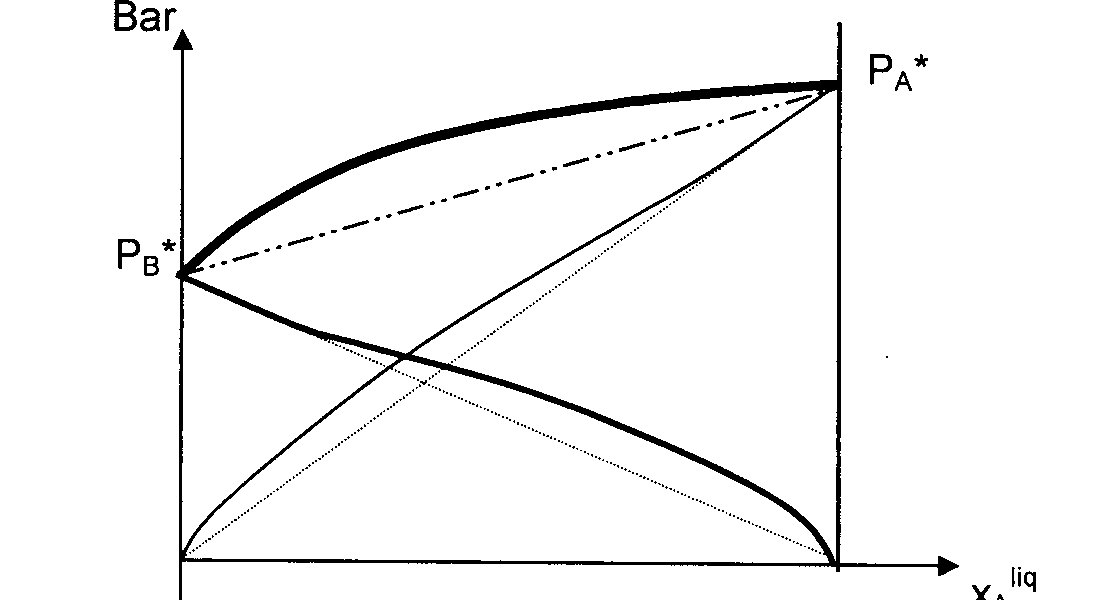
Non linéaire donc non idéal ou réel : (faire un schéma )
- La loi de Raoult n'est approximativement vérifiée que pour les solutions très concentrées en A , cad quand A est un solvant .
- On peut assimiler la partie de la courbe relative aux solutions très diluées en A à sa tangente : la pente = la constante de Henry : PA = Kh . xAliq
1/ Gaz parfait
à partir de ( ∂G/∂P)T = V ⇒ ( ∂μ/∂P)T = Vm et de la loi des gaz parfaits : démo du cours Le potentiel chimique d'un constituant, Le potentiel chimique d'un gaz, 1- Hypothèse gaz parfait
Potentiel standard de référence = potentiel du gaz sous 1 bar ( ⇒ standard) , pris comme référence ( si P= 1 bar , μ = μ° , si P ≠ P°, on raloute un terme correctif à μ° )
état de référence : état dans lequel l'espèce a un potentiel = μ° . Ici , gaz sous 1 bar.
2/ Corps pur condensé
Voir Le potentiel chimique d'un constituant, II-Le potentiel chimique d'un corps pur condensé
On repart de ( ∂μ/∂P)T = Vm avec Vm ≈ cte : intégration et expression et expression simplifiée .
3/ Mélanges idéaux et réels
Voir Le potentiel chimique d'un constituant, III-Le potentiel chimique en solution mélange, 2- les expressions du potentiel chimique et 3-
Bien distinguer :
IDEAL
NON IDEAL solvant / soluté / quelconque / soluté en solution aqueuse
Ecrire : μi(T,P) = μi°(T) + RT ln ai (+ Vm(P-P° ) ) avec toutes définitions de ai
III- Propriétés et applications
1/ Equilibre entre deux phases
Utiliser Gibbs Duhem ( Σnid μi(T,P) = 0 ) et l'équilibre dG =d (ni μi(T,P)) = 0 pour démontrer l'égalité du potentiel chimique en équilibre sous deux phases.
3/ Les lois de l'ébullioscopie, cryoscopie et osmose
Donner l'influence de T sur μ (pente -Sm, toujours plus faible de solide à liquide à gaz ), en déduire l'allure du graphe μ = f(T) . Faire le même pour un solvant ( soluté en faible quantité) (parallèle à la droite μliq mais plus basse car terme + RTln xA <0 )
Le solide formé à l'équilibre est supposé pur , la vapeur formée aussi (sous 1 bar) .
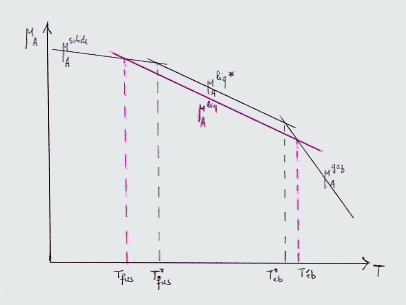
Montrer graphiquement que Téb augmente si présence du soluté . énoncer la loi de l'ébullioscopie .: "on peut montrer que " ΔT est proportionnel à la quantité de soluté dissoute , indépendamment de sa nature.
Montrer graphiquement que Tfus diminue si présence du soluté . énoncer la loi de la cryoscopie .: "on peut montrer que " ΔT est proportionnel à la quantité de soluté dissoute , indépendamment de sa nature.
Osmose pV = nRT à définir , selon le temps...
Voir TD pour les démos...