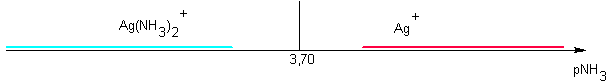Le but de cet exposé est de rappeler leur mode de construction et leur mode de lecture et donc leur intérêt .
Les courbes de dosage ne font pas partie de ce propos.
I- LES OUTILS GRAPHIQUES EN SOLUTIONS AQUEUSES
1- Acide/base
| Version mathématique | Version graphique |
| La constante de
l'équilibre
HA = A- +
H+est
notée KA
L'équilibre A/B obéit à la loi d'action des masses 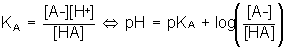 si pH < pKA c'est que [HA] > [A-] si pH > pKA +1 c'est que [A-] > 10 [HA] soit %A->90% si pH < pKA -1 c'est que [HA] > 10 [A-] soit %HA >90% Si pKA -1 < pH < pKA +1 => aucune prédominance >90% Cas d'un polycacide Cas de l'acide bichromate Dosage A/B Soit la réaction d'un acide faible sur une base faible : HA1/A1- de pKA1 et HA2/A2- de pKA2 Soit le mélange HA1 + A2- : La RP est : HA1 + A2- = HA2 + A1- K= KA1 / KA2 "deux" cas sont possibles :
Exemple mélanges Acide phosphorique / ammoniaque |
La constante de
l'équilibre HA
= A- +
H+est
notée KA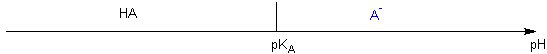 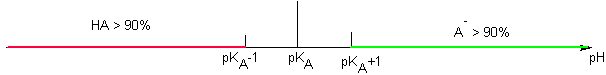 Soit la réaction d'un acide faible sur une base faible : HA1/A1- de pKA1 et HA2/A2- de pKA2 Soit le mélange HA1 + A2- : Cas n° 1 : ils n'ont pas de domaine commun : 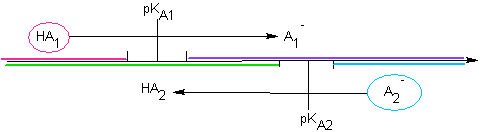 La réaction
est "totale" La réaction
est "totale"Soit le mélange HA1 + A2- : Cas n° 2 : ils ont un domaine commun : 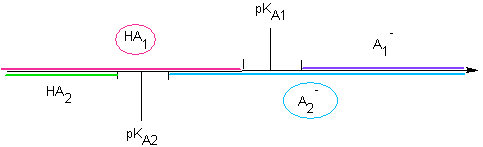 "Pas" de
réaction "Pas" de
réaction |
| Version mathématique | Version graphique |
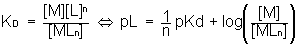 donc donc pL grand => domaine de M pL faible => domaine de MLn |
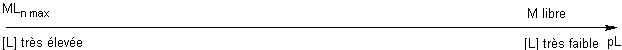 |
MAIS, pour un mélange constitué d'un cation métallique et d'un ligand, il existe souvent plusieurs complexes possibles.
Construire un axe de prédominance en complexation, c'est chercher la prédominance entre espèces obtenues successivement lors de l'ajout de ligand dans une solution d'ion métallique
Il faut distinguer les constantes de dissociation globales et les constantes de dissociation successives :
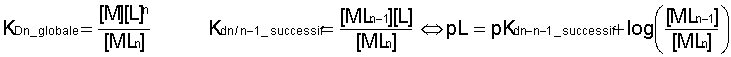
On montre que pour deux complexes successifs à n-1 ligands et n ligands, la constante Kdn/n-1 = KDn / KDn-1
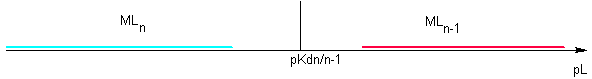
Dans cet exposé je noterai Kd les constantes de dissociation successives et KD les constantes de dissociation globales . Cette notation est circonstantielle, non officielle. On rencontre souvent β pour la notation des constantes de formation globale...
Exemple des complexes ammino cadmium II
Cas de complexes instables : ammino argent I
3- Précipitation ( et redissolution )
Nous travaillerons sur le précipité : MLn = Mn+ + n L- Ks constante de solubilité de ce complexe
Ce précipité sera éventuellement susceptible de se redissoudre sous la forme de MLm(m-n)- avec KD constante de dissociation globale du complexe
| Version mathématique | Version graphique |
| Soit
la formation
du précipité : Mn+
+ n L-
= MLn
K = 1/Ks EI : [ Mn+]o [L-] 0 (a=1) Pour que le précipité se forme il faut A>0 , à l'état initial =>Q<K soit [ Mn+ ][ L- ] > Ks => pL < pKs + log [ Mn+]o Soit la redissolution du précipité :
MLn
+
m-n L-
= MLm(m-n)-
K = Ks/KD
EI [ Mn+]o C 0 EF 0,ε (a=1) [ L- ]disp [ Mn+]o Donc à l'EF d'équilibre Ks/KD = [ Mn+]o / [ L- ]dispm-n => pLdisp =1/(m-n) ( pKD - pKs -log [ Mn+]o ) Cas d'un précipité avec les ions hydroxyde OH- Idem mais les axes sont tracés en pH au lieu de pOH => inversion des conditions : Formation : pH > pKs + log [ Mn+]o Redissolution : pH > pLdisp |
 Les pointillés rouges figurent les traces de Mn+ résiduelles en présence du précipité. 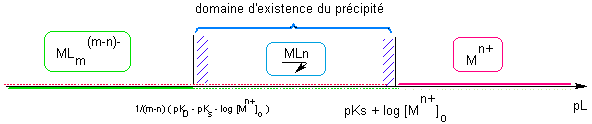  |
Dans le cas de précipitation entre un cation métallique et un anion basique dont la concentration dépend du pH ou autre cas similaire, on peut tracer des graphes bidimensionnels .
De façon courante, on trace les graphes log(solublité) / pH
"En fonction du pH" signifie que c'est l'expérimentateur qui se fixe le pH, par un moyen de son choix. Le plus simple est d'imaginer que l'on dissout le solide dans des solutions tampon de pH souhaité.
Méditer la différence avec la question : quel est le pH d'une solution obtenue par dissolution de n moles de ZnS dans 10 mL d'eau...par exemple....
On rappelle ici que la solubilité est la quantité maximale de solide dissous dans une solution à l'équilibre ( équilibre sous-entendant que le solide reste présent)
Deux exemples valent mieux ici qu'un long discours général :
Etude de la solubilité du sulfure de zinc en fonction du pH : Données ZnS = Zn2+ + S2- Ks H2S : KA1 = 7 KA2 = 13
| Etude mathématique | Résultat graphique | |
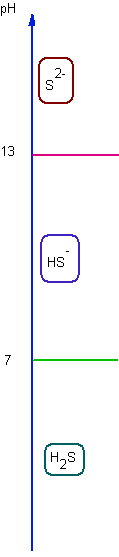 |
Q : Pourquoi la solubilité dépend-elle du pH ? Rép : car S2- est une base , dont la forme majoritaire varie selon le pH ( que l'on se fixera ) Conséquence : il existe 3 RP de solubilité: ZnS = Zn2+ + S2- Ks EI N 0 0 EF N - s s s (a=1) A l'équilibre, la LAM : Ks = s2 => log s = - 1/2 pKs ZnS + H+ = Zn2+ + HS- Ks / KA2 EI N h 0 0 EF N - s h s s h=
cte car on se fixe le pH
( tampon par exemple )
A l'équilibre , la LAM : Ks / KA2
= s2 / h => log s = 1/2 ( pKA2 - pKs) - 1/2 pH ZnS + 2H+ = Zn2+ + H2S Ks /( KA2 KA1) EI N h 0 0 EF N - s h s s h=
cte car on se fixe le pH
( tampon par exemple )
A l'équilibre , la LAM : Ks / ( KA2
KA1) = s2
/h2 => log s = 1/2 ( pKA2 + pKA1 - pKs) - pH |
L'axe
des ordonnées est à double lecture :
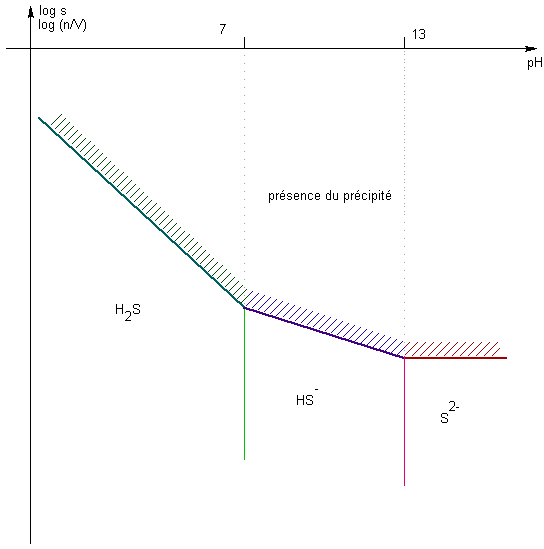 => au dessous du tracé, la quantité introduite < s => tout est dissous |
Bien sûr , on remarquera que la solubilité est plus forte en milieu acide , par consommation de l'ion sulfure par les ions H+ pour donner H2S , soit un déplacement de l'équilibre de solublité "primaire" ( définition du Ks )
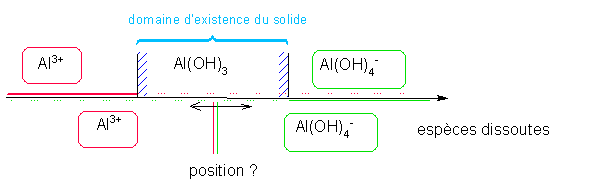
Etude de la solubilité de l'hydroxyde d'aluminium en fonction du pH : Données Al(OH)3 = Al3+ + 3 OH- pKs=32 Al(OH)4- = Al3+ + 4 OH- pKD = 33
| Etude mathématique | résultat graphique | |
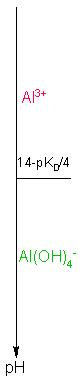 |
Q : pourquoi la
solubilité dépend-elle du pH? Rép : parce que 1) la quantité d'OH- est directement liée au pH ( que l'on se fixera ) 2) il existe un complexe en milieu fortement basique Conséquence : Il existe donc deux formes dissoutes de Al(OH)3 et donc deux réactions de dissolution Q : Domaines de pH des 2 formes dissoutes ??? Calcul préliminaire : Détermination des domaines de prédominance des 2 formes dissoutes Equilibre entre les deux formes dissoutes : Al(OH)4- = Al3+ + 4 OH- KD =[OH- ]4 [Al3+ ] / [ Al(OH)4- ] à l'équilibre Les
2 domaines de prédominance sont séparés par une frontière correspondant
à l'égalité entre les deux formes :
[Al3+
] = [ Al(OH)4-
]
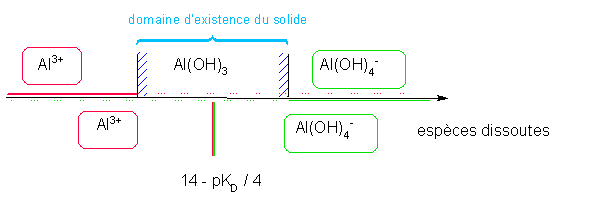
Donc à la frontière : KD =[OH- ]4 Soit pH = 14 - pKD / 4 Al(OH)3 = Al3+ + 3 OH- K = Ks EF Excès -s s θ θ=
cte car on se fixe le pH
( tampon par exemple ) A l'équilibre la LAM : Ks = θ3 . s = s . Ke3 / h3 => log s = ( 3 pKe - pKs ) - 3 pH Al(OH)3 + OH- = Al(OH)4-
K=Ks/KD EI Excès θ EF Excès - s θ s θ=
cte car on se fixe le pH
( tampon par exemple ) A l'équilibre la LAM : Ks / KD = s / θ = s. h / Ke => log s = ( pKd - pKs - pKe ) + pH |
  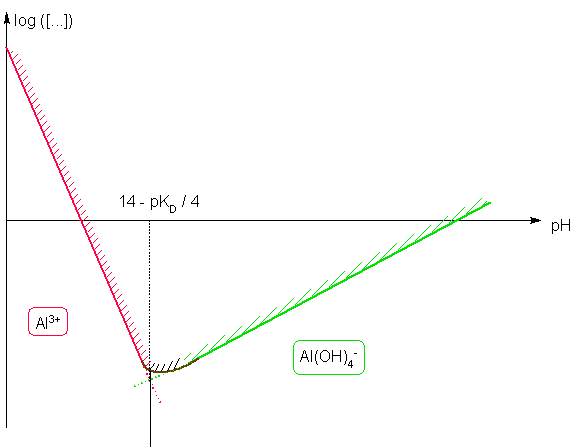 |
Suite...à venir...
Dans le cas des polyacides , il suffit d'étudier chaque couple successivement . Les espèces au centre du diagramme sont des ampholytes (à la fois acides et bases ) . Pour l'acide phosphorique voici ce que cela donne.
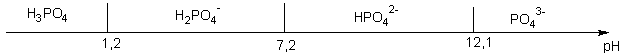
La lecture directe permet évidemment , si le pH de la solution est connu de savoir quelle est l'espèce majoritaire en solution (par exemple dans une solution tampon de pH =10, HPO42- est l'espèce majoritaire de l'acide phosphorique )
Très rares , certains acides ont une acidité multiple globale : c'est par exemple le cas pour le couple Cr2O72- / CrO42- , de pKA = 13,8
Ne perdons pas de vue que le schéma traduit la préominance de la base par rapport à l'acide : écrivons la réactions A/B élémentaire et la LAM associée :
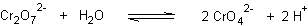 avec
avec 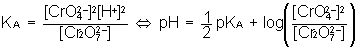
qui nous enseigne que la limite de prédominance n'est pas pKA mais 1/2 pKA en raison de la double acidité globale et que cette limite manifeste la prépondérance mathématique du CARRE de la concentration en base par rapport à la concentration en acide...soit :
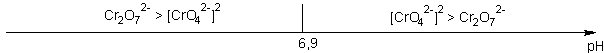
En dosage acide base, cette zone étroite de pH correspond au volume important nécessaire pour la consommation de 90% de l'espèce dosée :
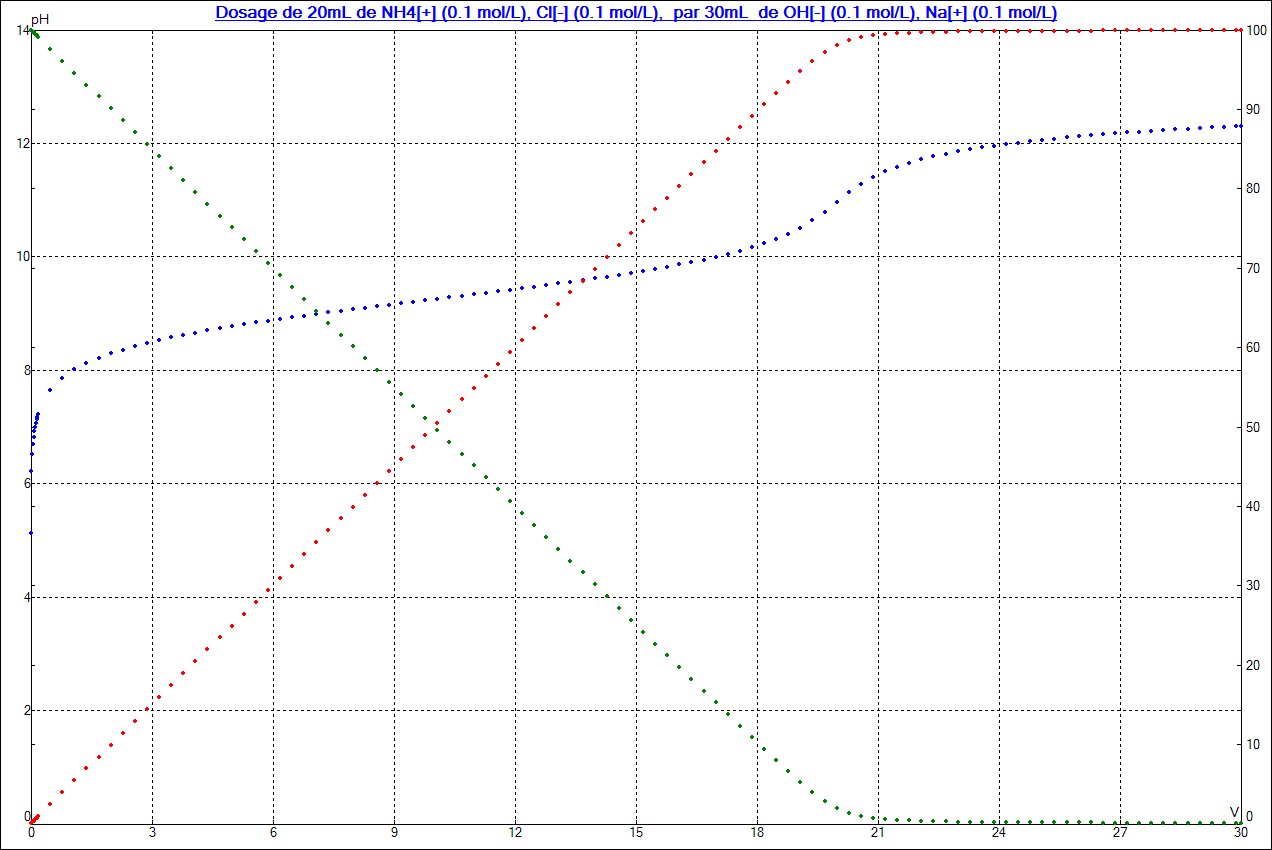
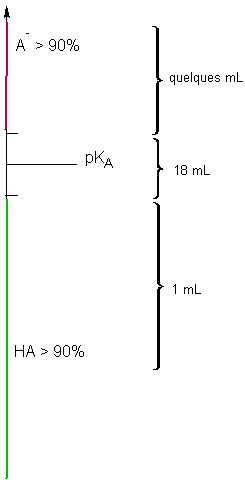
On remarquera que pendant la chute vertigineuse (variation linéaire ) de la quantité de NH4+ ( courbe verte) et donc par opposition la croissance identiquement vertigineuse ( et tout aussi linéaire) de la quantité de NH3 ( courbe rouge) le pH de la solution ( courbe bleue ) croit tout doucement (courbe bleue ) entre 8,2 et 10,2 .
On gardera donc en mémoire que pendant 18 mL qui constituent 90% du dosage ( consommation de NH4+ ), le pH varie fort peu.
Par contre , dans les deux premiers mL, ce pH a augmenté de façon drastique pendant la création des premiers 10% de NH3 . De même , ce pH croit brutalement pendant la disparition des derniers 10% de NH4+ : c'est la marque graphique de l'équivalence. Ces variations brutales du pH sont l'effet mathématique de la fonction log, utilisée pour marquer la proximité de la valeur ZERO pour l'une des variables du système ( au début pour NH3 et à l'équivalence pour NH4+ )
Soit un mélange d'acide phosphorique et d'ammoniac : Dessinons les axes correspondants
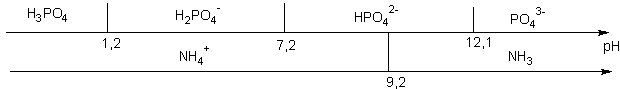
L'axe nous dit que la réaction entre H3PO4 et NH3 est totale H3PO4 + NH3 --> H2PO4- + NH4+
S'ils ont été introduits
en même quantité alors, le pH final sera dans le domaine commun des
espèces formées, soit H2PO4-
et NH4+,
donc compris entre 1,2 et 7,2 (proche de 4,2 )

S'ils ont été introduits avec le double d'ammoniac par rapport à
l'acide phosphorique, alors, comme H2PO4-
formé n'a pas de domaine commun avec l'ammoniac restant après la 1°
réaction ,il se produira en suivant la réaction suivante : H2PO4-
+ NH3
--> HPO42-
+ NH4+
; le pH final sera dans le domaine commun de HPO42-
et NH4+
soit entre 7,2 et 9,2 ( proche de 8,2)

Si NH3 est en quantité supérieure au double de l'acide phosphorique,
comme NH3 et HPO42-
ont un domaine commun, et que NH4+
est aussi présent, le pH sera proche de 9,2 selon la proportion en
excès / NH4+
d'ammoniac.




Nous prendrons dans cet exposé les données relatives à un mélange cadmium ammoniac en négligeant les propriétés basiques de l'ammoniac.
Les complexes qui existent sont les suivants : Cd(NH3)2+ , Cd(NH3)22+ , Cd(NH3)32+ , Cd(NH3)42+ , Cd(NH3)52+ , et Cd(NH3)62+
On donne pour chacun d'eux les pKD globale : 2,60 4,65 6,04 6,92 6,6 4,9
Donc pour le cadmium dans l'ammoniac, on obtient le résultat suivant :
| Cd(NH3)2+ | Cd(NH3)22+ | Cd(NH3)32+ | Cd(NH3)42+ | Cd(NH3)52+ | Cd(NH3)62+ | |
| pKDn | 2,60 | 4,65 | 6,04 | 6,92 | 6,6 | 4,9 |
| pKDn/n-1 | 2,60 | 2,05 | 1,39 | 0,88 | -0.32 | -1.7 |
Ce qui conduit à l'axe suivant :
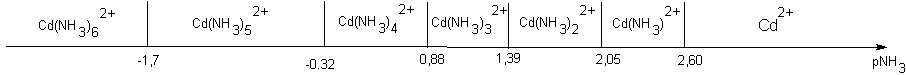
On remarquera qu'il n'existe aucune zone d'existence à + de 90% seul, pour aucun des complexes car il n'y a jamais plus de 2 unités d'écart entre les 2 valeurs limites .
D'autre part , les complexes hexa amminé ou penta amminé nécessitent des concentrations TRES fortes en ammoniac ; S'il sera possible d'obtenir le complexe penta ammino cadmium II, l'hexa ammino cadmium II sera TRES difficile à obtenir en solution aqueuse.
On trouve dans la littérature les données suivantes : Ag(NH3)+ pKD1 =3,40 Ag(NH3)2+ pKD2 = 7,40
Traçons l'axe de prédominance relatif à ces complexes de Ag+ en présence d'ammoniaque :
- Calcul des pKd ( successifs) : pKd1-0 = 3,40 pKd2-1 = 4
- Tracé de l'axe de prédominance : souci....:

2 Ag(NH3)+ ->
Ag(NH3)2+ + Ag+
Pour tracer le diagramme de prédominance, il ne faut donc pas tenir compte de Ag(NH3)+ , instable.
Les deux espèces à envisager sont donc Ag(NH3)2+ et Ag+ : limite pKD2 / 2 = 3,70 :